Contents
CHOLICM
Calculates a Cholesky-factor of the inverse covariance matrix (ICM) of a multivariable autoregressive process.
Syntax
C = cholicm(Af,Ab,Sf,Sb,N)
Description
The Inverse Covariance Matrix S of a multivariable autoregressive noise process according to [1] is calculated. A Cholesky factor C is returned such that C'C = S
The noise model contains a causal and an auticausal part, both of which describe the actual noise v(k). If e(k) is a Gaussian white innovation, the model is given by:
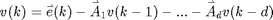
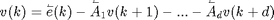
Right arrow denote the causal (Forward) components while left arrows denote the anti-causal (Backward) ones.
The multivariable noise model can be obtained using the destmar function
Inputs
Af is an l x ld matrix containing the causal part of the noise process. Af = [Af1,Af2,...,Afd]
Ab is an l x ld matrix containing the anti-causal part of the noise process. Ab = [Ab1,Ab2,...,Abd]
Sf is an l x l matrix describing the covariance E[ef ef']
Sb is an l x l matrix describing the covariance E[eb eb']
N is the number of samples
Outputs
C is a Cholesky factor of the ICM. This matrix is stored in LAPACK/BLAS band-storage; its size is (d + 1)l x N, and the bottom row contains the diagonal of C. The row above contains a zero, and then the first superdiagonal of C. The row above contains two zeros, and then the second superdiagonal, etc. The top row contains ((d + 1)l - 1) zeros, and then the ((d + 1)l - 1) th superdiagonal.
Limitations
A covariance matrix of a stationary process is always positive definite. However, it is very well possible to specify filter coefficients Af, Ab and covariances Sf and Sb such that the theoretical ICM calculated per [1] is not positive definite. In such cases, no Cholesky factor can be calculated, and an identity matrix will be returned along with a warning message. The filter should be checked and adjusted in these cases.
Algorithm
The upper-triangular block-band of a sparse banded inverse covariance matrix according to [1] is filled. A direct sparse Cholesky factorization is subsequently performed using MATLAB's internal chol function.
Used By
See Also
References
[1] B. Davis, Parameter Estimation in Nonlinear Dynamical Systems with Correlated Noise. PhD thesis, Universite Catholique de Louvain-La-Neuve, Belgium, 2001.