Contents

CSS2TH

Converts a parameter vector into a continuous-time LTI state-space model.

Syntax

[A,C] = cth2ss(theta,params)

[A,B,C] = cth2ss(theta,params)

[A,B,C,D] = cth2ss(theta,params)

[A,B,C,D,x0] = cth2ss(theta,params)

[A,B,C,D,x0,K] = cth2ss(theta,params)

Description

his function converts a parameter vector that describes a continuous-time state space model into the state space matrices of that model.

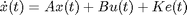
$$\dot{x}(t) = Ax(t) + Bu(t) + Ke(t)$$

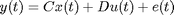
$$y(t) = Cx(t) + Du(t) + e(t)$$

Inputs

theta is the parameter vector describing the system.

params is a structure that contains the dimension parameters of the system, such as the order, the number of inputs and whether D, x0 or K is present.

T is the transformation matrix between the input state space system and the state space system in the form described by theta.

Outputs

A,B,C,D are system matrices describing the state space system. If theta does not contain parameters for D, this matrix will be returned as an empty matrix.

x0 is the initial state. If theta does not contain parameters for x0, this vector will be returned as an empty matrix.

K is the Kalman gain. If theta does not contain parameters for K, this vector will be returned as an empty matrix.

Remarks

This function is based on the SMI Toolbox 2.0 function cth2ss, copyright 1996 Johan Bruls. Support for the omission of D, x0 and/or K has been added, as well as support for the full parametrization.

Algorithm

The model parametrization for the output normal form and the tridiagonal parametrization is carried out according to [1]. The full model parametrization is a simple vectorization of the system matrices. In its most general form, the parameter vector is given by

Used By

foptlti, ffunlti

See Also

css2th, dth2ss

References

[1] B. Haverkamp, Subspace Method Identification, Theory and Practice. PhD thesis, Delft University of Technology, Delft, The Netherlands, 2000.


Published with MATLAB® R2012b