Contents

Example 18: Discretization of continuous LPV model of wing flutter

close all; clear; clc;

Wing flutter model

% Numerical values of parameters
a = -0.6847;
b = 0.135;
mw = 2.049;
mt = 12.387;
rho = 1.225;
ch = 27.43;
ca = 0.036;
cla = 6.28;
clb = 3.358;
cma = (0.5+a)*cla;
cmb = -0.635;
xa = (0.0873-(b+a*b))/b;
Ia = 0.0517+mw*xa^2*b^2;
kh = 2844.4;
ka = 2.84;

% System variables
d = (mt*Ia-mw^2*xa^2*b^2);

% System matrices for continuous-time
A0 = [0 0 1 0; 0 0 0 1;
    -Ia*kh/d +ka*mw*xa*b/d -Ia*ch/d +mw*xa*b*ca/d
    +mw*xa*b*kh/d -(mt/d)*ka +mw*xa*b*ch/d -mt*ca/d];
A1 = [0 0 0 0; 0 0 0 0;
    0 0 -(Ia*rho*b*cla+mw*xa*rho*b^3*cma)/d -(Ia*rho*b^2*cla*(0.5-a)+mw*xa*rho*b^4*cma*(0.5-a))/d;
    0 0 (mw*xa*rho*b^2*cla + mt*rho*b^2*cma)/d (mw*xa*rho*b^3*cla*(0.5-a)+mt*rho*b^3*cma*(0.5-a))/d];
A2 = [0 0 0 0; 0 0 0 0;
    0 -(Ia*rho*b*cla+mw*xa*b^3*rho*cma)/d 0 0;
    0 (mw*xa*b^2*rho*cla+mt*rho*b^2*cma)/d 0 0];

B0 = [0; 0; 0; 0];
B1 = [0; 0; 0; 0];
B2 = [0; 0; (-Ia*rho*b*clb-mw*xa*b^3*rho*cmb)/d; (mw*xa*b^2*rho*clb+mt*rho*b^2*cmb)/d];

sys = idafflpv([A0 A1 A2],[B0 B1 B2],[eye(2,4) zeros(2,4*2)],zeros(2,3));

Discretization of continuous LPV model

% discrete approximation
sysde1 = c2d(sys,0.05,'euler','linear');
sysde2 = c2d(sys,0.05,'euler','quadratic');
sysde3 = c2d(sys,0.05,'tustin','linear');
sysde4 = c2d(sys,0.05,'tustin','quadratic');

Discretization results

% scheduling signals
t = (0:0.01:0.1)';
v = linspace(1,12,length(t))';
p = [v v.^2];
pq = [v v.^2 v.^2 v.^3 v.^4];

% pole and zero locations
sys0 = idafflpv2ss(sys,p);
figure, pzmap(sys0);
syse1 = idafflpv2ss(sysde1,p);
syse2 = idafflpv2ss(sysde2,pq);
syse3 = idafflpv2ss(sysde3,p);
syse4 = idafflpv2ss(sysde4,pq);
figure, pzmap(syse1,'y',syse2,'g',syse3,'c',syse4,'b');

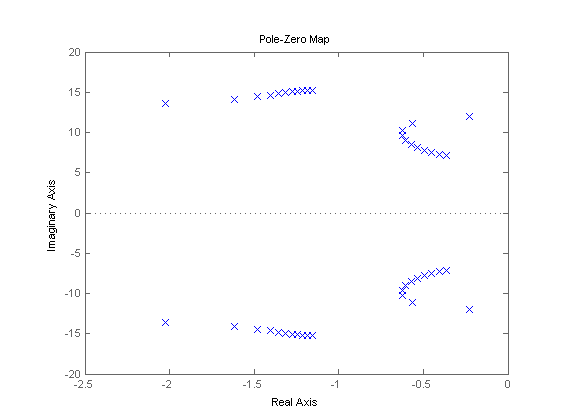
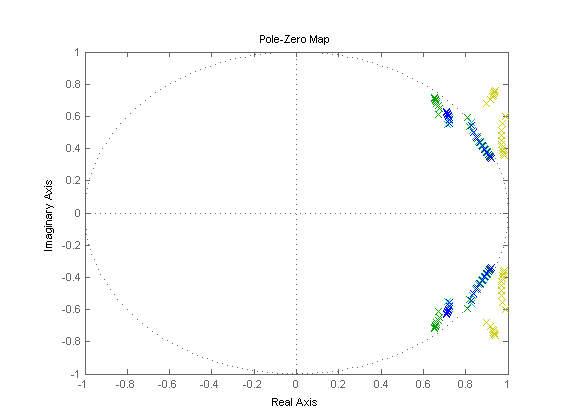
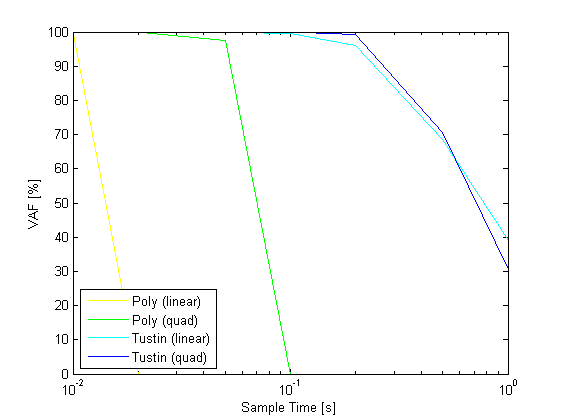
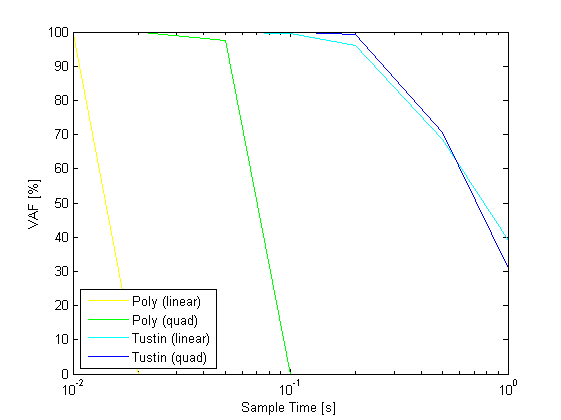
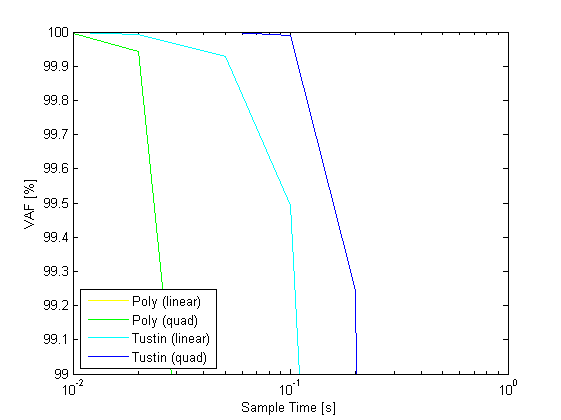
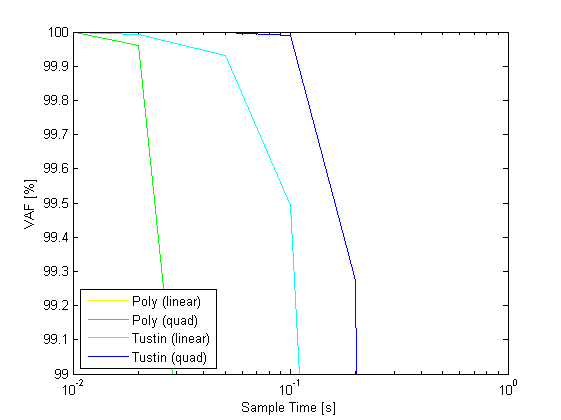
Performance of discretization

% discretization
Ts = [0.01 0.02 0.05 0.1 0.2 0.5 1];

% scheduling signals
t = (0:Ts(1):100)';
u = sin(0.2.*t);
v = linspace(1,12,length(t))';
p = [v v.^2];
pq = [v v.^2 v.^2 v.^3 v.^4];

% continuous simulation
[yc,tc] = sim(sys,u,t,p);

% euler approximation
sysde1 = c2d(sys,Ts(1),'euler','linear');
[ye1,te1] = sim(sysde1,u,t,p);
sysdeq1 = c2d(sys,Ts(1),'euler','quadratic');
[yeq1,teq1] = sim(sysdeq1,u,t,pq);

VAFE = zeros(2,length(Ts));
VAFT = zeros(2,length(Ts));
VAFE1 = zeros(2,length(Ts));
VAFT1 = zeros(2,length(Ts));
VAFEQ = zeros(2,length(Ts));
VAFTQ = zeros(2,length(Ts));
VAFE1Q = zeros(2,length(Ts));
VAFT1Q = zeros(2,length(Ts));
for j = 1:length(Ts);
    t = (0:Ts(j):100)';
    u = sin(0.2.*t);
    v = linspace(1,12,length(t))';
    p = [v v.^2];
    pq = [v v.^2 v.^2 v.^3 v.^4];

    % euler approximation
    sysde = c2d(sys,Ts(j),'euler','linear');
    [ye,te] = sim(sysde,u,t,p);

    % tustin approximation
    sysdt = c2d(sys,Ts(j),'tustin','linear');
    [yt,tt] = sim(sysdt,u,t,p);

    % euler approximation
    sysdeq = c2d(sys,Ts(j),'euler','quadratic');
    [yeq,teq] = sim(sysdeq,u,t,pq);

    % tustin approximation
    sysdtq = c2d(sys,Ts(j),'tustin','quadratic');
    [ytq,ttq] = sim(sysdtq,u,t,pq);

    ys = interp1q(tc,yc',t);
    ys1 = interp1q(te1,ye1,t);
    ysq1 = interp1q(teq1,yeq1,t);
    VAFE(:,j) = vaf(ys,ye);
    VAFT(:,j) = vaf(ys,yt);
    VAFE1(:,j) = vaf(ys1,ye);
    VAFT1(:,j) = vaf(ys1,yt);
    VAFEQ(:,j) = vaf(ys,yeq);
    VAFTQ(:,j) = vaf(ys,ytq);
    VAFE1Q(:,j) = vaf(ysq1,yeq);
    VAFT1Q(:,j) = vaf(ysq1,ytq);
end


figure,semilogx(Ts,mean(VAFE),'y',Ts,mean(VAFEQ),'g',Ts,mean(VAFT),'c',Ts,mean(VAFTQ),'b');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Location','SouthWest');

figure,semilogx(Ts,mean(VAFE1),'y',Ts,mean(VAFE1Q),'g',Ts,mean(VAFT1),'c',Ts,mean(VAFT1Q),'b');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Location','SouthWest');

figure,semilogx(Ts,mean(VAFE),'y',Ts,mean(VAFEQ),'g',Ts,mean(VAFT),'c',Ts,mean(VAFTQ),'b');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Location','SouthWest');
axis([0.01 1 99 100]);

figure,semilogx(Ts,mean(VAFE1),'y',Ts,mean(VAFE1Q),'g',Ts,mean(VAFT1),'c',Ts,mean(VAFT1Q),'b');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Location','SouthWest');
axis([0.01 1 99 100]);

Published with MATLAB® 7.9