Contents

Example 22: Third-order SIMO Periodic-LPV model

close all; clear; clc;

Periodic third-order LPV model

% System matrices
A1 = [0 0.9 0.2; -0.9 0.5 0; -0.2 0 0.2];
A2 = [0.60 -0.5 0.5; 0.50 0.60 0; -0.5 0 0.6];
A12 = [A1 A2];
B12 = [1 0.4; 1 0.2 ; 1 0.12];
C12 = [0.2 1 0.5 0.2 0.1 1; 0.2 0.1 1 0.3 0.4 0.8];
D12 = [0.1 0.2; 0.2 0.1];
K0 = [0.0130 0.0225; 0.0089 0.0060; 0.0002 -0.0010];

n = size(A12,1);    % The order of the system
m = size(A12,2)/n;  % The number of scheduling parameters
r = size(B12,2)/m;  % The number of inputs
l = size(C12,1);    % The number of outputs

Open-loop identification experiment

Simulation of the model in open loop

% Defining a number of constants
j = 18;     % period
np = 1000;  % number of periods
N = np*j;   % number of data points

% Measured data and the scheduling parameters
t = (0:N-1)';
u = randn(N,r);
mu1 = 0.8*sin(2*pi*(1:N)'./j) + 0.2;
mu3 = 0.8*cos(2*pi*(1:N)'./j) + 0.2;
mu = [mu1 mu3];

% Simulation of the system without noise
Alpv = [zeros(n) A12];
Blpv = [zeros(n,r) B12];
Clpv = [zeros(l,n) C12];
Dlpv = [zeros(l,r) D12];
Klpv = [K0 zeros(n,2*l)];
M = idafflpv(Alpv,Blpv,Clpv,Dlpv,Klpv,[],1);
y0 = sim(M,u,t,mu);

% Simulation of the system with noise
e = 0.1.*randn(N,l);
y = sim(M,u,t,mu,e);
disp('Signal to noise ratio (SNR) (open-loop)')
snr(y,y0)

Signal to noise ratio (SNR) (open-loop)

ans =

   21.1911   19.1111

Identification of the model in open loop

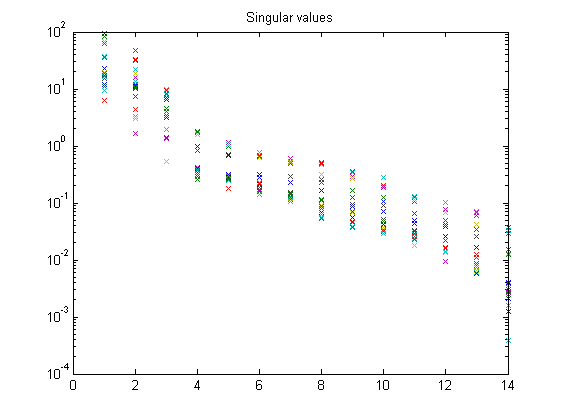
% Defining a number of constants
p = 7;     % past window size
f = 7;     % past window size

% LPV identification without noise
pnd = pschedclust(mu,f,p);
[S,X,TU,K] = pordvarx(u,y,mu,f,p,pnd,'tikh','gcv',0,[0 0 0 0 1]);
[x,CC] = pmodx(X,TU,K,n,1e-4,1e-8);
[A,B,C,D,K] = px2abcdk(x,u,y,mu,f,p,[0 0 0 0 1],pnd);
figure, semilogy(S,'x');
title('Singular values')
disp('Canonical correlation coefficients')
CC(1:n)

Canonical correlation coefficients

ans =

    0.9993    0.9988    0.9957

Verification results

% Simulation of identified LPV system
Aidm = [zeros(n) A];
Bidm = [zeros(n,r) B];
Cidm = [zeros(l,n) C];
Didm = [zeros(l,r) D];
Kidm = [zeros(n,l) K];
Mm = idafflpv(Aidm,Bidm,Cidm,Didm,Kidm,[],1);
yidm = sim(Mm,u,t,mu);
disp('VAF of identified LPV system')
vaf(y,yidm)

VAF of identified LPV system

ans =

   98.7543
   98.1991

Published with MATLAB® 7.9