MSc Thesis Proposal
Optimal control of linear hybrid systems
with saturation
Mentors: B. De
Schutter
Prerequisites: research oriented attitude
of the student
Keywords: hybrid systems, control, optimization
Description:
Hybrid systems arise from the interaction between
continuous variable systems (i.e.,
systems that can be described by a difference or differential
equation) and discrete event
systems (i.e.,
systems where the state transitions are initiated by events that occur
at discrete time instants).
In general we could say that a hybrid system
can be in one of several "regimes" whereby in each regime
the behavior of the system can be described by a
system of difference or differential equations,
and that the system switches from one regime to another due to the occurrence
of events (see Figure 1).
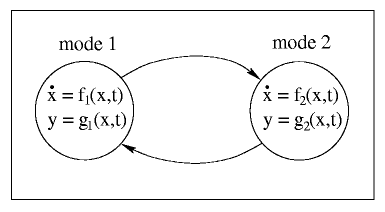
Figure 1: A schematic representation of a hybrid system with
two regimes.
Up to now there are no useful modeling and control techniques
that can be applied to general hybrid systems
and that are still tractable.
Therefore, we consider a special class of hybrid systems
in this research proposal: the class of linear hybrid systems
with saturation. In each regime the evolution of such a
system can be described by linear difference or differential
equations, possibly with saturation at some upper or lower bounds.
Typical examples of this kind of systems
are traffic light controlled intersections
or systems consisting
of several fluid containers that are connected by tubes
with valves.
The control objective is to determine the optimal
switching time instants from one regime to another.
In some cases this problem can be solved analytically
whereas in other cases numerical optimization
is required to determine the optimal switching scheme.
The aim of this research proposal is to develop
efficient methods to compute optimal switching schemes
for (subclasses of) linear hybrid systems with saturation.
If you are interested in selecting this project as your MSc project,
please come along or send us an email for more information.
This page is maintained by
Bart De Schutter.

