Contents

Example 8: Uncertainty bounds on estimation using Bootstrap simulations

close all; clear; clc;

LTI model of a Coleman tranformed wind turbine system

% LTI system matrices
h = 0.1;             % Sample time
[OL,CL] = wtsLTI(h); % The wind turbine model
n = size(OL.a,1);    % The order of the system
r = size(OL.b,2);    % The number of inputs
l = size(OL.c,1);    % The number of outputs

Closed-loop identification experiment

Simulation of the model in closed loop

% Number of monte carlo simulations
MCS = 100;

% Time sequence
N = 10000;  % number of data points
t = (0:h:h*(N-1))';

% Wind disturbance signals
d = randn(N,3);

% Excitation signal for pitch input
r_pitch = randn(N,1);

% Excitation signal for Torque input
r_torque = 1e3.*randn(N,1);

% Add together for simulation
r = [r_pitch zeros(N,2) r_torque zeros(N,2)];

% Simulation of the closed-loop system
y = lsim(CL,[d r],t);

% Input and output selaction with scaling
ui = detrend(y(:,7:8),'constant');   % selects input for identification (excitation of pitch + control)
yi = detrend(y(:,1:3),'constant');   % selects output for identification
ri = [r_pitch r_torque];
[us,Du,ys,Dy] = sigscale(ui,yi); % signal scaling
Dat = iddata(ys',us',h);
ys0 = ys;
Dat0 = Dat;

% Frequency grid
w = logspace(-2,log10(pi/h),1000);

% Allocate storage vectors
VAF = zeros(MCS,3);
EE = zeros(MCS,7);

for nmcs = 1:MCS
    disp(['Simulation ', num2str(nmcs)])

    % Defining a number of constants
    p = 50;     % past window size
    f = 20;     % future window size

    % PBSID-opt
    [S,x] = dordvarx(us,ys,f,p,'tikh','gcv');
    x = dmodx(x,n);
    [Ai,Bi,Ci,Di,Ki] = dx2abcdk(x,us,ys,f,p,'stable');
    EE(nmcs,:) = eig(Ai);
    Dat = iddata(ys',us',h);
    Mi = abcdk2idss(Dat,Ai,Bi,Ci,Di,Ki);

    % Variance-accounted-for (by Kalman filter)
    yest = predict(Mi,Dat0);
    vfm = vaf(ys0,yest.y);

    % bootstrapping
    [e,x0] = pe(Mi,Dat0);
    y0 = sim(Mi,[zeros(N,2) e.y]);
    ys = ys0 - y0';
    ye = sim(Mi,zeros(N,2),'Noise');
    ys = ys + ye';

    % store results
    sys = ss(Ai,Bi/Du,Dy*Ci,Dy*Di/Du,h);
    if nmcs == 1
        Hmin = abs(freqresp(sys,w));
        Hmax = abs(freqresp(sys,w));
        H0 = abs(freqresp(sys,w));
    else
        Hmin = min(abs(Hmin),abs(freqresp(sys,w)));
        Hmax = max(abs(Hmax),abs(freqresp(sys,w)));
    end
    VAF(nmcs,:) = vfm';
end

Simulation 1
Forcing matrix A to be stable.
Simulation 2
Simulation 3
Simulation 4
Forcing matrix A to be stable.
Simulation 5
Simulation 6
Simulation 7
Simulation 8
Simulation 9
Simulation 10
Simulation 11
Simulation 12
Simulation 13
Simulation 14
Simulation 15
Simulation 16
Forcing matrix A to be stable.
Simulation 17
Simulation 18
Simulation 19
Simulation 20
Simulation 21
Simulation 22
Simulation 23
Simulation 24
Simulation 25
Simulation 26
Simulation 27
Simulation 28
Simulation 29
Simulation 30
Simulation 31
Simulation 32
Simulation 33
Simulation 34
Simulation 35
Simulation 36
Simulation 37
Simulation 38
Simulation 39
Simulation 40
Simulation 41
Simulation 42
Simulation 43
Simulation 44
Simulation 45
Simulation 46
Simulation 47
Simulation 48
Simulation 49
Simulation 50
Simulation 51
Simulation 52
Simulation 53
Simulation 54
Simulation 55
Simulation 56
Simulation 57
Simulation 58
Simulation 59
Simulation 60
Simulation 61
Simulation 62
Simulation 63
Simulation 64
Simulation 65
Simulation 66
Simulation 67
Simulation 68
Simulation 69
Simulation 70
Simulation 71
Simulation 72
Simulation 73
Simulation 74
Simulation 75
Simulation 76
Simulation 77
Simulation 78
Simulation 79
Simulation 80
Simulation 81
Simulation 82
Simulation 83
Simulation 84
Simulation 85
Simulation 86
Simulation 87
Simulation 88
Simulation 89
Simulation 90
Simulation 91
Simulation 92
Simulation 93
Simulation 94
Simulation 95
Simulation 96
Simulation 97
Simulation 98
Simulation 99
Simulation 100

Identification results

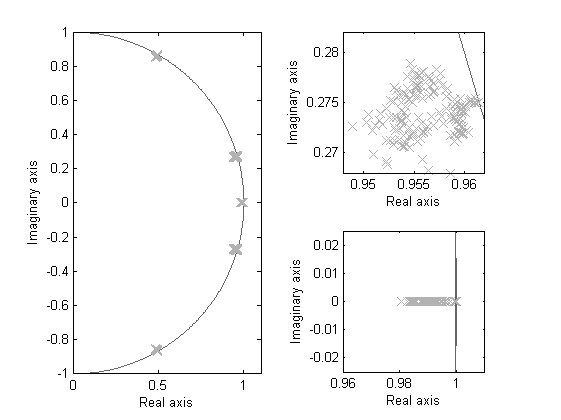
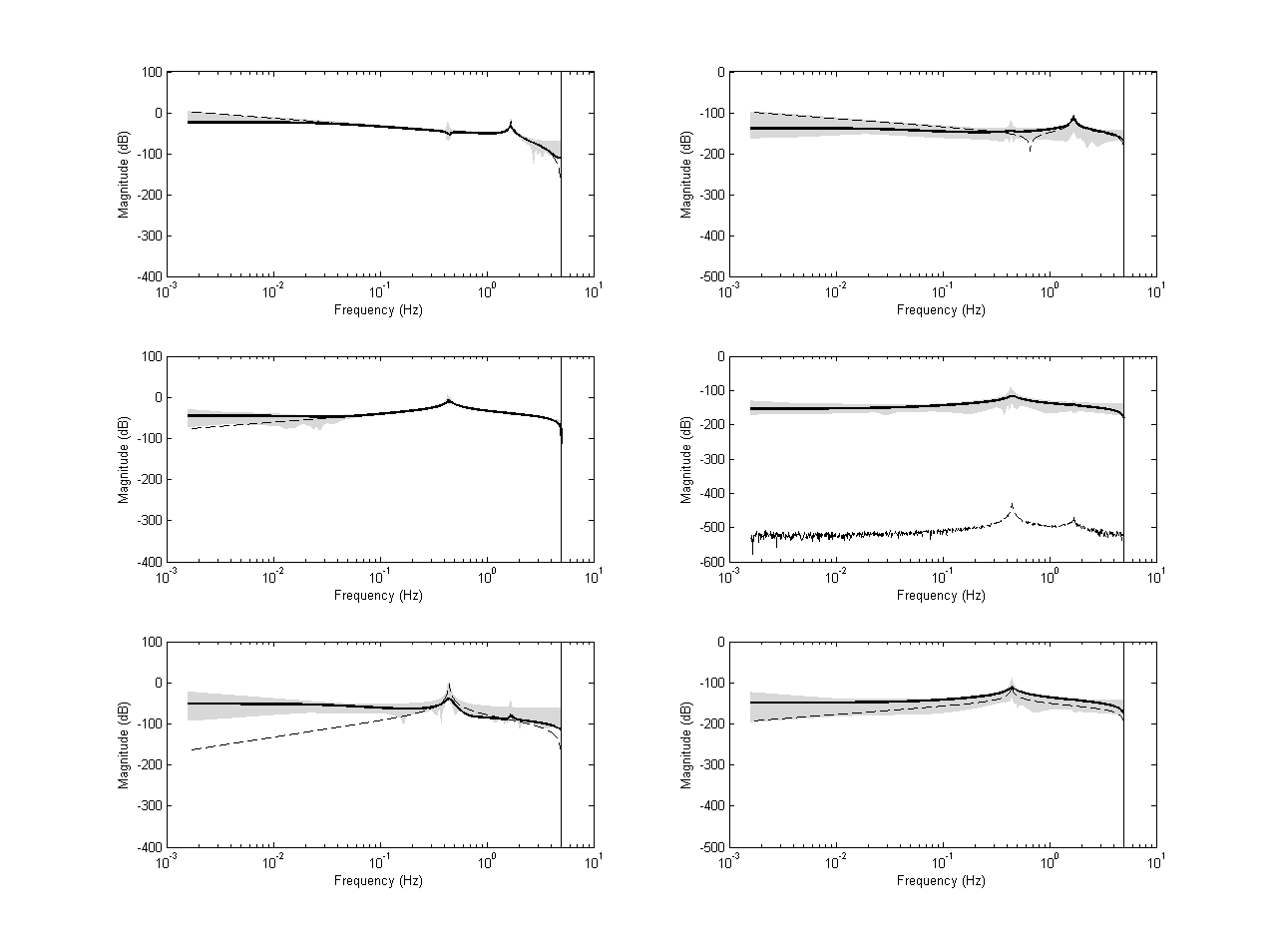
% Plot eigenvalues
realeig = eig(minreal(OL(1:5,[4 7])));
figure, subplot(2,2,[1 3]), deigen(EE',realeig);
axis([0 1.1 -1 1]);
subplot(2,2,2), deigen(EE',realeig);
axis([0.948 0.962 0.268 0.282]);
subplot(2,2,4), deigen(EE',realeig);
axis([0.96 1.01 -0.025 0.025]);

% frequency response of identified system
Hr = abs(freqresp(minreal(OL(1:5,[4 7])),w));
figure('Units','normalized','Position',[0 0 1 1]), hold on
dbodemagpatch(H0,Hmin,Hmax,w,h,Hr);
hold off

Published with MATLAB® 7.9.1