Contents

Example 17: Discretization of continuous LPV model of F-16

close all; clear; clc;

F-16 VISTA Flight Model

For model see [1]

% continuous-model
A0 = [0.22 1; 17.1 -0.228];
A1 = [-4.10e-7 0; -8.07e-4 7.06e-6];
A2 = [-2.6 0; -68.4 -2.12];
A3 = [5.15e-5 0; 3.31e-3 4.86e-5];
A4 = [0 0; 56.2 0];
A5 = [0 0; -2.92e-3 0];
B0 = [-1.38e-3; -8.16];
B1 = [8.75e-8; 1.73e-4];
B2 = [-0.34; 40.6];
B3 = [7.89e-6; -8.96e-4];
B4 = [0; -99.3];
B5 = [0; 2.42e-3];
C0 = eye(2);

% make affine lpv system
sys = idafflpv([A0 A1 A2 A3 A4 A5],[B0 B1 B2 B3 B4 B5],[C0 zeros(2,5*2)],zeros(2,6),...
    'statename',{'alpha' 'q'},'schedulingname',{'h' 'M' '(h*M)' '(M^2)' '(h*M^2)'},...
    'inputname','elevator','outputname',{'angle-of-attack' 'pitch-rate'},'Name','F16 Aircraft');

Discretization of continuous LPV model

% discrete approximation
sysde1 = c2d(sys,0.05,'euler','linear');
sysde2 = c2d(sys,0.05,'euler','quadratic');
sysde3 = c2d(sys,0.05,'tustin','linear');
sysde4 = c2d(sys,0.05,'tustin','quadratic');

Discretization results

% scheduling signals
t = (0:0.05:1)';
M = linspace(0.4,0.6,length(t))';
h = linspace(5000,25000,length(t))';
p = [h M h.*M M.^2 M.^2.*h];
pq = [h M h.*M M.^2 M.^2.*h  h.*h h.*M h.*h.*M h.*M.^2 h.*M.^2.*h...
    M.*M M.*h.*M M.*M.^2 M.*M.^2.*h  h.*M.*h.*M h.*M.*M.^2 h.*M.*M.^2.*h...
    M.^2.*M.^2 M.^2.*M.^2.*h  M.^2.*h.*M.^2.*h];

% pole and zero locations
sys0 = idafflpv2ss(sys,p);
figure, pzmap(sys0);
syse1 = idafflpv2ss(sysde1,p);
syse2 = idafflpv2ss(sysde2,pq);
syse3 = idafflpv2ss(sysde3,p);
syse4 = idafflpv2ss(sysde4,pq);
figure, pzmap(syse1,'y',syse2,'g',syse3,'c',syse4,'b');

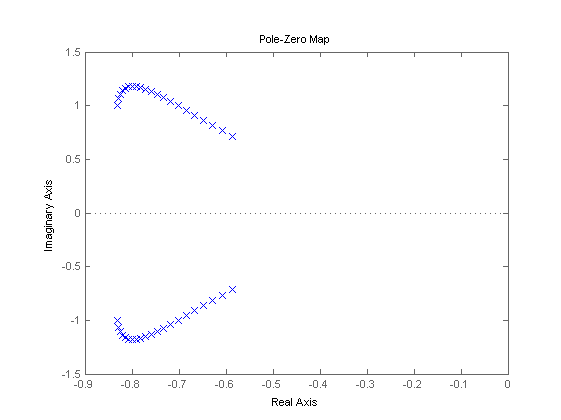
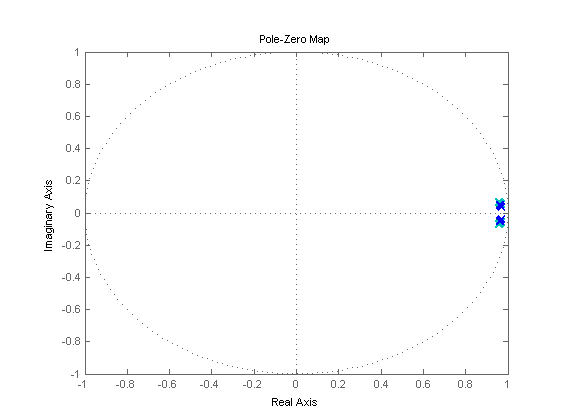
Performance of discretization

% sample times
Ts = [0.01 0.02 0.05 0.07 0.1 0.2 0.5 0.7 1];

% scheduling signals
t = 0:Ts(1):100;
u = sin(0.2.*t)';
M = linspace(0.4,0.6,length(t))';
h = linspace(5000,25000,length(t))';
p = [h M h.*M M.^2 M.^2.*h];
pq = [h M h.*M M.^2 M.^2.*h  h.*h h.*M h.*h.*M h.*M.^2 h.*M.^2.*h...
    M.*M M.*h.*M M.*M.^2 M.*M.^2.*h  h.*M.*h.*M h.*M.*M.^2 h.*M.*M.^2.*h...
    M.^2.*M.^2 M.^2.*M.^2.*h  M.^2.*h.*M.^2.*h];

% continuous simulation
[yc,tc] = sim(sys,u,t,p);

% euler approximation
sysde1 = c2d(sys,Ts(1),'euler','linear');
sysdeq1 = c2d(sys,Ts(1),'euler','quadratic');
[ye1,te1] = sim(sysde1,u,t,p);
[yeq1,teq1] = sim(sysdeq1,u,t,pq);

n = 1;
VAFZ = zeros(2,length(Ts));
VAFE = zeros(2,length(Ts));
VAFT = zeros(2,length(Ts));
VAFZ1 = zeros(2,length(Ts));
VAFE1 = zeros(2,length(Ts));
VAFT1 = zeros(2,length(Ts));
VAFEQ = zeros(2,length(Ts));
VAFTQ = zeros(2,length(Ts));
VAFE1Q = zeros(2,length(Ts));
VAFT1Q = zeros(2,length(Ts));
for j = 1:length(Ts);
    t = 0:Ts(j):100;
    u = sin(0.2.*t)';
    M = linspace(0.4,0.6,length(t))';
    h = linspace(5000,25000,length(t))';
    p = [h M h.*M M.^2 M.^2.*h];
    pq = [h M h.*M M.^2 M.^2.*h  h.*h h.*M h.*h.*M h.*M.^2 h.*M.^2.*h...
        M.*M M.*h.*M M.*M.^2 M.*M.^2.*h  h.*M.*h.*M h.*M.*M.^2 h.*M.*M.^2.*h...
        M.^2.*M.^2 M.^2.*M.^2.*h  M.^2.*h.*M.^2.*h];

    % symbolic
    sysdz = c2d(sys,Ts(j),'zoh','linear');
    [yz,tz] = sim(sysdz,u,t',p);

    % euler approximation
    sysde = c2d(sys,Ts(j),'euler','linear');
    [ye,te] = sim(sysde,u,t',p);

    % tustin approximation
    sysdt = c2d(sys,Ts(j),'tustin','linear');
    [yt,tt] = sim(sysdt,u,t',p);

    % euler approximation
    sysdeq = c2d(sys,Ts(j),'euler','quadratic');
    [yeq,teq] = sim(sysdeq,u,t',pq);

    % tustin approximation
    sysdtq = c2d(sys,Ts(j),'tustin','quadratic');
    [ytq,ttq] = sim(sysdtq,u,t',pq);

    ys = interp1q(tc,yc',t');
    ys1 = interp1q(te1,ye1,t');
    ysq1 = interp1q(teq1,yeq1,t');
    VAFZ(:,j) = vaf(ys,yz);
    VAFE(:,j) = vaf(ys,ye);
    VAFT(:,j) = vaf(ys,yt);
    VAFZ1(:,j) = vaf(ys1,yz);
    VAFE1(:,j) = vaf(ys1,ye);
    VAFT1(:,j) = vaf(ys1,yt);
    VAFEQ(:,j) = vaf(ys,yeq);
    VAFTQ(:,j) = vaf(ys,ytq);
    VAFE1Q(:,j) = vaf(ysq1,yeq);
    VAFT1Q(:,j) = vaf(ysq1,ytq);
end

figure,semilogx(Ts,VAFEQ(1,:),'y',Ts,mean(VAFE),'g',Ts,mean(VAFT),'c',Ts,mean(VAFTQ),'b',Ts,mean(VAFZ),'r');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Symbolic (linear)','Location','SouthWest');

figure,semilogx(Ts,mean(VAFE1),'y',Ts,mean(VAFE1Q),'g',Ts,mean(VAFT1),'c',Ts,mean(VAFT1Q),'b',Ts,mean(VAFZ1),'r');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Symbolic (linear)','Location','SouthWest');

figure,semilogx(Ts,mean(VAFE),'y',Ts,mean(VAFEQ),'g',Ts,mean(VAFT),'c',Ts,mean(VAFTQ),'b',Ts,mean(VAFZ),'r');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Symbolic (linear)','Location','SouthWest');
axis([0.001 1 99 100]);

figure,semilogx(Ts,mean(VAFE1),'y',Ts,mean(VAFE1Q),'g',Ts,mean(VAFT1),'c',Ts,mean(VAFT1Q),'b',Ts,mean(VAFZ1),'r');
xlabel('Sample Time [s]')
ylabel('VAF [%]')
legend('Poly (linear)','Poly (quad)','Tustin (linear)','Tustin (quad)','Symbolic (linear)','Location','SouthWest');
axis([0.001 1 99 100]);

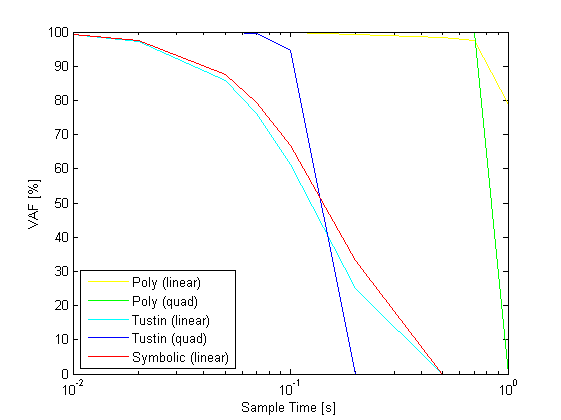
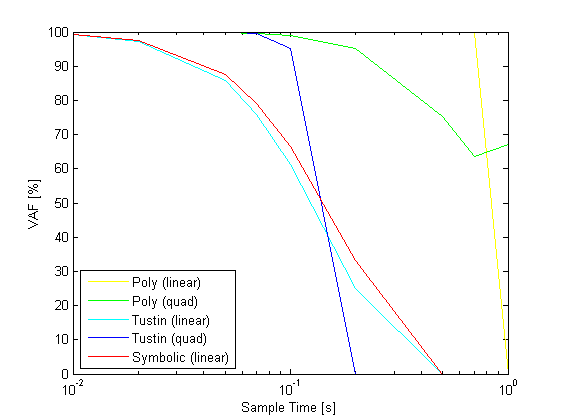
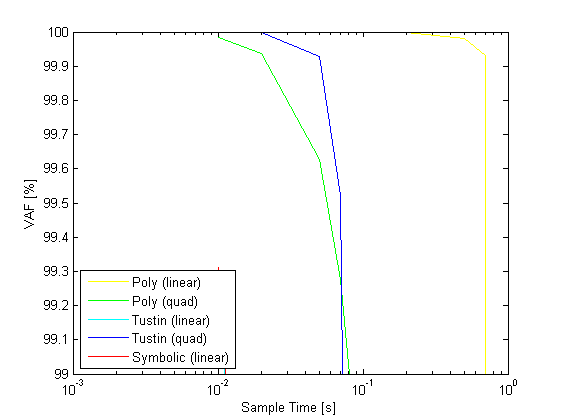
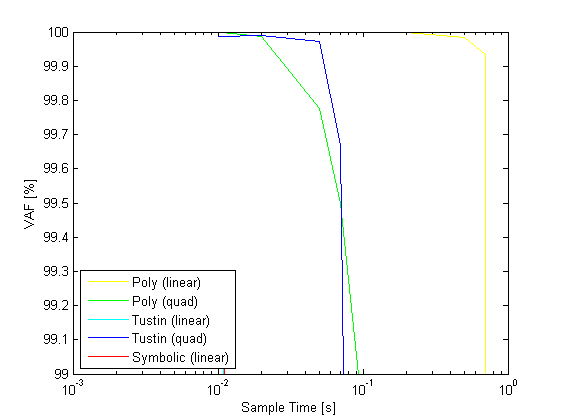
References

[1] M. Spillman, P. Blue, S. Banda, and L. Lee, "A Robust Gain-Scheduling Example Using Linear Parameter-Varying Feedback," Proc. of the 13th IFAC World Congress, San Francisco, vol. H, pp. 221-226, 1996

Published with MATLAB® 7.9