Contents
DINIT
Estimates the initial state, given estimated discrete-time state-space system matrices and a batch of measured input-output data.
Syntax
x0 = dinit(A,B,C,D,u,y)
Description
This function estimates the initial state for a measured input-output batch of a discrete-time LTI state-space model. The estimate is based on the measured input-output data sequences, and on the A, B, C and D matrices, which are possibly estimated using any of the subspace identification functions.
Inputs
A,B,C,D is the discrete-time LTI state-space model.
u,y is the measured input-output data from the system to be identified.
Outputs
x0 is the estimated initial state.
Algorithm
Estimating the initial state x0 from input-output data and the system matrices is a linear regression [1]:
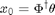
The regression matrix Phi and data matrix theta are given by:

in which yhatk) is simulated using the estimated system matrices and the measured input u(k). The function ltiitr is used to efficiently calculate yhat(k).
Used By
This a top-level function that is used directly by the user.
Uses Functions
See Also
References
[1] B. Haverkamp, Subspace Method Identification, Theory and Practice. PhD thesis, Delft University of Technology, Delft, The Netherlands, 2000.