Contents
LTIITR
Calculates an LTI state-trajectory
Syntax
x = ltiitr(A,B,u,w,x0)
Description
In its most general setting, this function iterates the state equation of an linear time-inavriant (LTI) system. It computes the state x(k) for k = 1,2,...,N satisfying the LTI state equation:
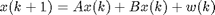
This function is used internally by dfunlti, dac2b, dac2bd, dinit and dltisim. It is not meant for stand-alone use.
Inputs
A is an LTI state-transition matrix of size n x n
B is an LTI input matrix of size n x m.
u is a N x m matrix containing N samples of the m inputs.
w is a (optional) N x n matrix containing the process noise.
x0 is the (optional) initial state, an n x 1 vector.
Outputs
x is the computed state, an N x n matrix.
Algorithm
A direct iteration of the system's state-transition equation is used to obtain the state-trajectory for all time-instants.
Used By
dfunlti, dac2b, dac2bd, dinit, dltisim