Contents
DSS2TH
Converts a discrete-time LTI state-space model into a parameter vector.
Syntax
[theta,params,T] = dss2th(A,C,partype)
[theta,params,T] = dss2th(A,B,C,partype)
[theta,params,T] = dss2th(A,B,C,D,partype)
[theta,params,T] = dss2th(A,B,C,D,x0,partype)
[theta,params,T] = dss2th(A,B,C,D,x0,K,partype)
Description
This function converts a discreter-time LTI state-space model into a parameter vector that describes the model. Model structure:
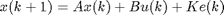
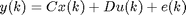
Inputs
A,B,C,D are system matrices describing the state space system. The B and D matrices are optional and can be left out or passed as an empty matrix to indicate it is not part of the model.
x0 is the (optional) initial state.
K is the (optional) Kalman gain.
partype is string which specifies the type of parameterization that is used to parameterize the state space model. Three types of parameterization are supported:
- 'on' for output Normal parametrization.
- 'tr' for tridiagonal parametrization.
- 'fl' for full parametrization.
Rules for input parameters:
- The final parameter should always be the parametrization type. The order for the parameters prior to partype is A,B,C,D,x0,K. The only exception is A,C, when only those are to be parametrized.
- All parameters after A,B,C and before partype are optional. If the last one is not to be parametrized it can be omitted. If any other is not to be parametrized, an empty matrix should be passed.
- (A,B,C,partype) is thus equivalent to (A,B,C,[],[],[],partype) However, (A,B,C,[],x0,partype) cannot be abbreviated.
Outputs
theta is the parameter vector describing the system.
params is a structure that contains the dimension parameters of the system, such as the order, the number of inputs and whether D, x0 or K is present.
T is the transformation matrix between the input state space system and the state space system in the form described by theta.
Remarks
This function is based on the SMI Toolbox 2.0 function dss2th, copyright 1996 Johan Bruls. Support for the omission of D, x0 and/or K has been added, as well as support for the full parametrization.
Algorithm
The model parametrization for the output normal form and the tridiagonal parametrization is carried out according to [1]. The full model parametrization is a simple vectorization of the system matrices. In its most general form, the parameter vector is given by

Used By
See Also
References
[1] B. Haverkamp, Subspace Method Identification, Theory and Practice. PhD thesis, Delft University of Technology, Delft, The Netherlands, 2000.