foptlti

FOPTLTI
Syntax
Description
Inputs
Outputs
Remarks
Used By
Uses Functions
See Also
References

FOPTLTI

Performs a frequency-domain nonlinear least squares optimization of an LTI state-space model.

Syntax

[A,B,C,D] = foptlti(H,w,A,B,C,D)

[A,B,C,D,options] = foptlti(H,w,A,B,C,D,model,partype,options)

Description

This function performs a nonlinear least squares optimization of a discrete or continuous time linear state space model based on frequency reponse data. The model structure is the following:

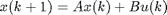
$$ x(k+1) = Ax(k) + Bu(k) $$

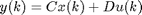
$$ y(k) = Cx(k) + Du(k) $$

First, the state space matrices are parameterized. The output normal parametrization, the tridiagonal parametrization and the full parametrization can be used.

The parameterized model is optimized using the supplied lmmore Levenberg-Marquardt function. The matrices A, B, C and D are returned.

Inputs

H is the measured frequency response function (FRF). This should be a matrix which follows the convention of MATLAB 6; it should be l x m x N in which H(:,:,i) contains the complex FRF at the i th complex frequency.

w is the vector of complex frequencies at which the FRF is measured. Although the function can operate using arbitrary complex frequencies, the following two choices are rather standard for discrete and continuous time models respectively:

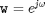
$\mathtt{w} = e^{j\omega}$

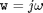
$\mathtt{w} = j\omega$

A,B,C,D is the initial estimates of the system matrices A, B, C and D.

partype is the (optional) parameter which specifies the type of parameterization that is used to parameterize the state space model. Three types of parameterization are supported:

'on' for output Normal parametrization.
'tr' for tridiagonal parametrization.
'fl' for full parametrization.

options are the (optional) input parameters that are passed on directy to the optimization function. These options may be compatible with the optimset options from the MATLAB 6 Optimization Toolbox [1]. Alternatively, a MATLAB 5 Optimization Toolbox compatible foptions vector may be specified.

There are a number of fields in addition to the normal fields in the options structure. These are described in detail in the remarks section below.

timing must be either 'cont' or 'disc' to specify that the model is continuous or discrete time. Note that this changes only the stability check and the output normal parametrization. It is up to the user to supply suitable frequency data.

Outputs

A,B,C,D are the system matrices of the optimized linear model. If the D matrix is not estimated, it will be returned empty.

options are the output parameters from the Optimization Toolbox. See foptions or optimset.

Remarks

An extra field options.Manifold may be set to 'on' if the full parametrization is used. The Manifold field indicates whether the search direction should be confined to directions in which the cost-function changes.

If options.Manifold is not set, foptlti will set it to 'off' for the output normal and tridiagonal parametrizations, and to 'on' for the full parametrization. See foptions or optimset for more information.

Another new field that can be set is the options.BlockSize field. The value Nb of the BlockSize field indicates that the Jacobian in the cost-function is build up Nb block-rows at a time rather than all at once [2]. This option is mainly interesting in tight-memory situations or for problems with a very large number of samples. If options.BlockSize is set to Nb, the fields options.RFactor and options.LargeScale are set to 'on' automatically. A rule of thumb is that the Jacobian-calculation requires about 24(p + 1 + 2 Nb l m)(p + 1) bytes of computer memory, in which p is the number of free parameters. For the full parametrization, this is the number of parameters after an optional Manifold-projection.

This optimization function has been targeted at MATLAB version 6 or higher. However, the function will run on MATLAB version 5 using a compatibility kludge. This kludge implies that the options input parameter can either be a MATLAB 6 optimset-structure, or a MATLAB 5 compatible foptions-vector. However, the latter is discouraged since it does not allow the Manifold, LargeScale, RFactor and BlockSize fields to be set.

Used By

This is a top-level function that is used directly by the user.

Uses Functions

lmmore, dss2th, dth2ss, css2th, ffunlti

References

[1] The MathWorks Inc., Natick, Massachusetts, Optimization Toolbox User's Guide, version 2.1 (release 12) ed., Sept 2000.

[2] N. Bergboer, V. Verdult, and M. Verhaegen, "An effcient implementation of maximum likelihood identification of LTI state-space models by local gradient search", in Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, Nevada, Dec. 2002.

Contents