Contents
DMODPO
Estimates the A and C matrices and the Kalman gain in a discrete-time state-space model from time-domain data that was preprocessed by dordpo.
Syntax
[A,C] = dmodpo(R,n)
[A,C,K] = dmodpo(R,n)
[A,C,K] = dmodpo(R,n,'stable')
Description
This function estimates the A and C matrices corresponding to an n th order discrete-time LTI state-space model. A Kalman gain can be estimated as well. The compressed data matrix R from the preprocessor function dordpo is used to this end.
Inputs
R is a compressed data matrix containing information about the measured data, as well as information regarding the system dimensions.
n is the desired model order n..
stable estimates a stable A matrix, see [2].
Outputs
A is the state-space model's A matrix.
C is the state-space model's C matrix.
K is the Kalman gain matrix.
Remarks
The data matrix R generated by the M-file implementation of dordpo is incompatible with the R matrix generated by the MEX-implementation of dordpo. Therefore, either the M-files should be used for both dordpo and dmodpo, or the MEX-files should be used for both functions. The stable option only works in the M-file implementation/
The MEX-implementation of dmodpo uses the IB01BD function from the SLICOT library.
The MEX-implementation may generate the following warning:
Warning: Covariance matrices are too small: returning K=0
This implies that there is not enough information available to reliably estimate a Kalman gain. K = 0 is returned for stability reasons in this case.
Algorithm
The data matrix obtained with dordpi contains the weighted left singular vectors of the R32 matrix. The first n of these vectors form an estimate Os of the system's extended observability matrix:

The estimates Ahat and Chat are obtained by linear regression:
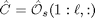
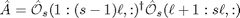
The optional Kalman gain is aclculated based on estimated noise covariance matrices [1].
Used By
This a top-level function that is used directly by the user.
See Also
dordpo, dordpi, dmodpi, dordrs, dmodrs,
References
[1] M. Verheagen, "Identification of the deterministic part of MIMO state space models given in innovations form from input-output data", Automatica, vol. 30, no. 1, pp. 61-74, 1994.
[2] J.M. Maciejowski, "Guaranteed Stability with Subspace Methods", Submitted to Systems and Control Letters, 1994.