Contents

DORDRS

Preprocesses time-domain data for the iterative Reconstructed State RS-MOESP algorithm to identify discrete-time state-space models. Delivers an order-estimate.

Syntax

[S,R] = dordrs(u,y,x,s)

[S,R] = dordrs(u,y,x,s,Rold)

Description

This function performs the initial data compression for RS-MOESP subspace identification based on measured input-output data [1] and a reconstructed state from a previous model estimate [1]. In addition, it delivers information usuable for determining the required model order. The model structure is the following

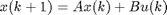
$$ x(k+1) = Ax(k) + Bu(k) $$

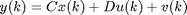
$$ y(k) = Cx(k) + Du(k) + v(k) $$

Here, v(k) is zero-mean noise of arbitary color, independent of the noise-free input u(k) . Several data batches can be concatenated, as shown below. This function acts as a preprocessor to dmodrs.

Inputs

u,y is the measured input and output data of the system to be identified.

x is the reconstructed state. This state can be obtained by simualting the state0equation belonging to the previous model estimate's Ahat and Bhat matrices:

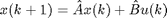
$$ x(k+1) = \hat{A} x(k) + \hat{B} u(k) $$

This initial model can be obtained by e.g. PI-MOESP.

s is the block-size parameter. This scalar should be >n.

Rold is the (optional) data-matrix resulting from a previous call to dordrs.

Outputs

S is the first s singular values of the rank-deficient R32 matrix (see below).

R is a compressed data matrix containing information about the measured data, as well as information regarding the system dimensions.

Algorithm

The discrete-time data compression algorithm in [1] is used. The following RQ-factorization is made:

The meaning of the various matrices can be found in the cited article. A weighted SVD of the R32 matrix is made, and its left singular vectors are appended to the R-matrix. Its first s singular values are returned in S.

Used By

This a top-level function that is used directly by the user.

See Also

dordpo, dmodpo, dordpi, dmodpi, dmodrs

References

[1] M. Verheagen, "Identification of the deterministic part of MIMO state space models given in innovations form from input-output data", Automatica, vol. 30, no. 1, pp. 61-74, 1994.


Published with MATLAB® R2012b