Contents
FAC2B
Estimates the B matrix in discrete-time and continuous-time state-space models from frequency response function (FRF) data, the D matrix is assumed to be zero.
Syntax
B = fac2b(A,C,H,w)
B = fac2b(A,C,H1,w1,...,Hp,wp)
Description
This function estimates the B matrix corresponding to a discrete-time or continuous-time LTI state-space model. The estimate is based on the measured frequency response function (FRF) data, and on the A and C matrices, which are possibly estimated using fdmodom or fcmodom. The D matrix is assumed to be zero. Several data batches can be concatenated, though this is possible for discrete-time models only.
Inputs
A is the state-space model's A matrix.
C is the state-space model's C matrix.
H is the measured frequency response function (FRF). This should be a matrix which follows the convention of MATLAB 6; it should be l x m x N in which H(:,:,i) contains the complex FRF at the i th complex frequency.
w is the vector of complex frequencies at which the FRF is measured. Although the function can operate using arbitrary complex frequencies, the following two choices are rather standard for discrete and continuous time models respectively:

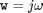
For discrete-time models, multiple data batches can be concatenated by appending additional H, w pairs to the parameter list.
Outputs
B is the state-space model's B matrix.
R is a compressed data matrix that can be used to concatenate another data batch in a subsequent call to fac2b (discrete-time models only).
Algorithm
Estimating B from the frequency response function (FRF) data and A and C is a linear regression [1]:

The regression matrix Phi and data matrix theta are given by:

The function ltifrf is used to efficiently fill the regression matrix Phi.
Used By
This a top-level function that is used directly by the user.
Uses Functions
See Also
fac2bd, fdmodom, fcmodom, ltifrf
References
[1] T. McKElvey, H. Akcay, and L. Ljung, "Subspace-based multivariable system identification from frequency response data", IEEE Transactions on Automatic Control, vol. 41, pp. 960-979, July 1996.