dfunlti

DFUNLTI
Syntax
Description
Inputs
Outputs
Algorithm
Used By
Uses Functions
See Also
References

DFUNLTI

Calculates the cost-function information for doptlti.

Syntax

[epsilon] = dfunlti(th,u,y,params)

[epsilon,psi] = dfunlti(th,u,y,params)

[epsilon,psi,U2] = dfunlti(th,u,y,params)

[epsilon] = dfunlti(th,u,y,params,options,OptType,sigman,filtera,CorrD)

[epsilon,psi] = dfunlti(th,u,y,params,options,... OptType,sigman,filtera,CorrD)

[epsilon,psi,U2] = dfunlti(th,u,y,params,options,... OptType,sigman,filtera,CorrD)

Description

This function implements the cost-fuction for doptlti. It is not meant for standalone use.

Inputs

th is the parameter vector describing the system.

u,y is the input and output data of the system to be optimized.

params is a structure that contains the dimension parameters of the system, such as the order, the number of inputs, whether D, x0 or K is present in the model.

options is an (optional) optimset compatible options-structure. The fields options.RFactor, options.LargeScale, options.Manifold and options.BlockSize should have been added by doptlti.

OptType (optional) indicates what kind of weighted least squares or maximum likelihood optimization is being performed:

'no_mle' implies a nonlinear (weighted) least squares optimization.
'uncorr' implies a maximum likelihood optimization without correlation among the output perturbances [1].
'flcorr' implies a maximum likelihood optimization with correlated output perturbances [2].

sigman (optional) If OptType is 'no_mle', this can be a vector of size 1 x l that indicates the standard deviation of the perturbance of each of the outputs. If OptType is 'uncorr', this should be a vector of size 1 x l that indicates the standard deviation of the white noise innovations for the output perturbance AR model. If OptType is 'flcorr', this should be a Cholesky factor of the AR process' inverse covariance matrix, as obtained by cholicm.

filtera (optional) If OptType is 'uncorr', this should be the A-polynomial of a d th order AR noise model. The first element should be 1, and the other elements should be d filter coefficients. In the multi-output case filtera should be a matrix having max(di)+1 rows and l columns. If a certain output noise model has a lower order, then the coefficient vector should be padded with |NaN|s.

CorrD (optional) If OptType is 'uncorr', this should be a correction matrix for the lower-right part of the ICM's Cholesky-factor. No details will be provided here.

Outputs

epsilon is the output of the cost function, which is the square of the error between the output and the estimated output.

psi is the Jacobian

$\Psi_N$

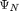
of epsilon, or

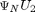
$\Psi_N U_2$

if the full parametrization is used.

U2 is the left null-space of Manifold matrix for the full parametrization [3].

Algorithm

The formation of the error-vector is done by simple simulation of the current model:

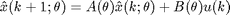
$\hat{x}(k+1;\theta) = A(\theta) \hat{x}(k;\theta) + B(\theta) u(k)$

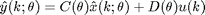
$\hat{y}(k;\theta) = C(\theta) \hat{x}(k;\theta) + D(\theta) u(k)$

The error-vector

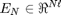
$E_N \in \Re^{N \ell}$

is build up such that its i th blockrow consists of

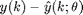
$y(k)-\hat{y}(k;\theta)$

Note that this example corresponds to the error-vector of an output error model in which no output weighting is applied. For innovation models and maximum likelihood corrections, the error-vector is different from the one shown above.

The Jacobian is formed by simulation as well [4]. This is a special case of the Jacobian for LPV systems that has been described in [3]. A QR-factorization is used to obtain its left null-space.

Used By

doptlti (via lmmore)

Uses Functions

dth2ss, itritr, simlns

References

[1] B. David and G. Bastin, "An estimator of the inverse covariance matrix aqnd its application to ML parameter estimation in dynamical systems", Automatica, vol. 37, no. 1, pp. 99-106, 2001.

[2] B. Davis, Parameter Estimation in Nonlinear Dynamical Systems with Correlated Noise. PhD thesis, Universite Catholique de Louvain-La-Neuve, Belgium, 2001.

[3] L.H. Lee and K. Poolla, "Identification of linear parameter varying systems using nonlinear programming", Journal of Dynamic Systems, Measurement and Control, col. 121, pp. 71-78, Mar 1999.

[4] N. Bergboer, V. Verdult, and M. Verhaegen, "An effcient implementation of maximum likelihood identification of LTI state-space models by local gradient search", in Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, Nevada, Dec. 2002.

Contents