Contents
FFUNLTI
Calculates the cost-function information for foptlti.
Syntax
[epsilon] = ffunlti(th,H,params,timing)
[epsilon,psi] = ffunlti(th,H,params,timing)
[epsilon,psi,U2] = ffunlti(th,H,params,timing)
Description
This function implements the cost-fuction for foptlti frequency domain optimization framework. It is not meant for standalone use.
Inputs
th is the parameter vector describing the system.
H is the frequency response function of the system to be optimized: an array of size l x m x N in which H(:,:,i) contains the complex FRF at the i th complex frequency.
w are the complex frequencies at which the FRF is measured.
params is a structure that contains the dimension parameters of the system, such as the order, the number of inputs, whether D, x0 or K is present in the model.
timing must be either 'cont' or 'disc', indicating that the supplied model is continuous of discrete time. Note that this influences only the way in which the output normal parametrization is built. The user is responsible for supplying suitable frequency data.
Outputs
epsilon is the output of the cost function, which is the square of the error between the output and the estimated output.
psi is the Jacobian of epsilon.
U2 is the left null-space of Manifold matrix for the full parametrization [1].
Algorithm
The formation of the error-vector is done bu calculating the FRF of the current model:
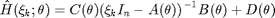
The error-vector

is build up such that its i th blockrow consists of
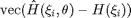
, in which the real and imaginary components have been interleaved.
The Jacobian is formed efficiently by calculating FRFs as well. The formation of the Manifold matrix is performed according to [1]. A QR-factorization is used to obtain its left null-space.
Used By
Uses Functions
See Also
References
[1] L.H. Lee and K. Poolla, "Identification of linear parameter varying systems using nonlinear programming", Journal of Dynamic Systems, Measurement and Control, col. 121, pp. 71-78, Mar 1999.