Contents

LTIFRF

Calculates an LTI Frequency Response Function

Syntax

H = ltifrf(A,B,C,[],[],w,outopt)

H = ltifrf(A,B,C,D,[],w,outopt)

H = ltifrf([],[],[],D,[],w,outopt)

H = ltifrf(A,B,C,[],dA,w,outopt)

Description

ltifrf will return the Frequency Response Function (FRF) of a linear time-invariant state-space model, evaluated at the complex frequencies provided in w:

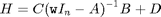
$$H = C {(\mathtt{w} I_n - A)}^{-1} B + D$$

This function is used internally by ffunlti, fac2b and fac2bd. It is not meant for stand-alone use.

Inputs

A is the state-space model matrix A.

B is the state-space model matrix B.

C is the state-space model matrix C.

D is the (optional) state-space model matrix D.

dA (optional) calculates the change in FRF given the deviation dA in A. D and dA are mutually exclusive.

w is the vector of complex frequencies. For discrete-time systems:

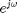
$$e^{j\omega}$$

and for continuous-time systems.

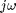
$$ j\omega $$

outopt controls how H will be returned (see below).

Outputs

H is the FRF. Usually a 3D-array of size l x m x N. However, if outopt is non-empty and 1, H will be a vector of size lmN x 1. If outopt is non-empty and 2, H will be a matrix of size l x mN.

Algorithm

The state-space model is first transformed such that its state-transistion matrix A is in upper-Hessenberg form. The matrix

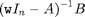
$${(\mathtt{w} I_n - A)}^{-1} B$$

is subsequently solved by an efficient upper-Hessenberg solver in SLICOT, after which premultiplication by C and addition of D yields the FRF. This approach follows [1].

If a deviation deltaA in A is given, the FRF deviation is given by:

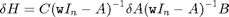
$$ \delta H = C {(\mathtt{w} I_n - A)}^{-1} \delta A {(\mathtt{w} I_n - A)}^{-1} B $$

Again, the model is transformed so that A has upper-Hessenberg form, after which the SLICOT Hessenberg solver is used to obtain

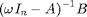
$${(\omega I_n - A)}^{-1} B$$

and

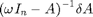
$${(\omega I_n - A)}^{-1} \delta A$$

Multiplication then yeilds the FRF deviation.

Used By

ffunlti, dac2b, dac2bd

Uses Functions

SLICOT-functions MB02RZ, MB02SZ, TB05AD

LAPACK-functions DGEHRD and DORMHR

(All built into the executable)

See Also

ffunlti, fac2b, fac2bd

References

[1] A.J. Laub, "Efficient multivariable frequency response calculations", IEEE Transactions on Automatic Control, vol. 26, pp. 407-408, Apr. 1981.


Published with MATLAB® R2012b