Contents
DOPTLTI
Performs a nonlinear least squares or maximum likelihood optimization of a discrete time LTI state space model.
Syntax
[A,B,C,D] = doptlti(u,y,A,B,C,D)
[A,B,C,D,x0,K,options] = doptlti(u,y,A,B,C,D,x0,K,... partype,options,sigman,nmodel)
Description
This function performs a nonlinear least squares optimization of a discrete time linear state space system model with structure
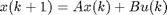
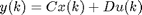
The function also supports innovation models:
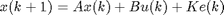
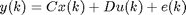
First, the state space matrices are parameterized. The output normal parametrization, the tridiagonal parametrization and the full parametrization can be used.
The parameterized model is optimized using the supplied lmmore Levenberg-Marquardt function. The matrices A, B, and C are always returned. If needed, D, the initial state and a Kalman gain can also be optimized.
Inputs
u,y is the input and output data of the system to be optimized.
A,B,C,D is the initial estimates of the system matrices A, B, C and D.
x0 is the (optional) initial state
K is the (optional) Kalman gain
partype (optional) This parameter specifies the type of parameterization that is used to parameterize the state space model. Three types of parameterization are supported:
- 'on' for output Normal parametrization.
- 'tr' for tridiagonal parametrization.
- 'fl' for gull parametrization.
options (optional) Input parameters that are passed on directy to the optimization function. These options may be compatible with the optimset options from the MATLAB 6 Optimization Toolbox [1]. Alternatively, a MATLAB 5 Optimization Toolbox compatible foptions vector may be specified.
There are a number of fields in addition to the normal fields in the options structure. These are described in detail in the remarks section below.
sigman (optional) The function of this parameters depends on its format:
- If sigman is a 1 x l vector, the output errors will be weighted by the inverse of these factors. In a weighted least squares estimation, sigman should contain the standard deviations of the noise on each of the outputs. In a maximum likelihood estimation which assumes no correlation between the noise on different outputs [2], sigman should contain the standard deviations of the white-noise signals which, when put through the AR filter specified by nmodel, generates the output measurement noise.
- If sigman is an l x 2l matrix, a maximum likelihood estimation which does support correlation between the output noises will be carried out [3]. The nmodel parameter must be specified in this case. sigman should be [Sf Sb], in which Sf is the covariance matrix of the multivariable white noise sequence that is put through the causal filter Af (see nmodel). Sb is the covariance matrix of the white noise sequence that will be put through the anticausal filter Ab.
nmodel (optional) The specification of the AR noise model. This should be either a matrix of size d x l, or a matrix of size 2l x ld, for an AR model of order d . In the first output case nmodel should be a matrix having a number of rows equal to the highest noise-model order on any of the outputs. The matrix should have l columns. If a certain output noise model has a lower order, then pad the coefficient vector with NaN s. In the second case, filtera should be [Sf Sb] in which Af specifies the causal AR filter, and Ab specifies the anti- causal AR filter, as obtained using cholicm.
Outputs
A,B,C,D are the system matrices of the optimized linear model. If the D matrix is not estimated, it will be empty.
x0 is the estimate of the initial state. If the x0 matrix is not estimated, it will be returned empty.
K is the estimate of the Kalman gain. If the K matrix is not estimated, it will be returned empty.
options are the output parameters from the Optimization Toolbox. See foptions or optimset.
Remarks
An extra field options.Manifold may be set to 'on' if the full parametrization is used. The Manifold field indicates whether the search direction should be confined to directions in which the cost-function changes. If options.Manifold is not set, doptlti will set it to 'off' for the output normal and tridiagonal parametrizations, and to 'on' for the full parametrization.
Another new field that can be set is the options.BlockSize field. The value Nb of the BlockSize field indicates that the Jacobian in the cost-function is build up Nb block-rows at a time rather than all at once [4]. This option is mainly interesting in tight-memory situations or for problems with a very large number of samples. If options.BlockSize is set to Nb, the fields options.RFactor and options.LargeScale are set to 'on' automatically. A rule of thumb is that the Jacobian-calculation requires about 24(p + 1 + Nb l)(p + 1) bytes of computer memory, in which p is the number of free parameters. For the full parametrization, this is the number of parameters after a manifold-projection.
If the model is unstable one can use the innovation description. This implies choosing a K such that (A - KC) is stable. The first option is to just specify K in the parameter list. This starts a prediction error optimization in which K is optimized as well. Faster convergence can be obtained by restricting K to a fixed value. To this end, the field options.OEMStable should be set to 'on', in addition to specifying K in the parameter list.
This optimization function has been targeted at MATLAB version 6 or higher. However, the function will run on MATLAB version 5 using a compatibility kludge. This kludge implies that the options input parameter can either be a MATLAB 6 optimset-structure, or a MATLAB 5 compatible foptions-vector. However, the latter is discouraged since it does not allow the Manifold, LargeScale, RFactor, BlockSize and OEMStable fields to be set.
Limitations
The doptlti-function is a non-linear optimization. This implies that there is the inherent risk of ending up in a local minimum, rather than in the cost-function's global minimum. Therefore, a well-chosen initial model should be used. If the optimization gets stuck in a local minimum nontheless, a different initial model should be tried.
An initial estimate can be obtained by using the time-domain subspace identification functions in this toolbox. The relevant functions are dordpo, dmodpo, dordpi, dmodpi, dordrs, dmodrs, dac2b and dac2bd.
Used By
This is a toplevel function that is used directly by the user.
Uses Functions
lmmore, dss2th, dth2ss, dfunlti, cholicm
See Also
foptlti, optimset, foptions, mkoptstruc
References
[1] The MathWorks Inc., Natick, Massachusetts, Optimization Toolbox User's Guide, version 2.1 (release 12) ed., Sept 2000.
[2] B. David and G. Bastin, "An estimator of the inverse covariance matrix aqnd its application to ML parameter estimation in dynamical systems", Automatica, vol. 37, no. 1, pp. 99-106, 2001.
[2] B. Davis, Parameter Estimation in Nonlinear Dynamical Systems with Correlated Noise. PhD thesis, Universite Catholique de Louvain-La-Neuve, Belgium, 2001.
[4] N. Bergboer, V. Verdult, and M. Verhaegen, "An effcient implementation of maximum likelihood identification of LTI state-space models by local gradient search", in Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, Nevada, Dec. 2002.